Let 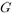 be a cyclic group with generator
be a cyclic group with generator  . The discrete logarithm problem with auxiliary inputs (DLPwAI) is asked to find
. The discrete logarithm problem with auxiliary inputs (DLPwAI) is asked to find 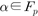 with auxiliary inputs
with auxiliary inputs  ,
, 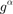 ,…,
,…, 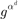 . In Eurocrypt 2006, an algorithm is proposed to solve DLPwAI in
. In Eurocrypt 2006, an algorithm is proposed to solve DLPwAI in 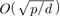 when
when 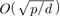 . In this paper, we reduce the DLPwAI to the problems to find polynomials with small value sets or to find efficiently.
. In this paper, we reduce the DLPwAI to the problems to find polynomials with small value sets or to find efficiently.
In this talk, we propose a new approach to solve DLPwAI concentrating on the behavior of function mapping between the finite fields rather than using an embedding to auxiliary groups. This result shows the relation between the complexity of the algorithm and the number of absolutely irreducible factors of the substitution polynomials, hence enlightens the research on the substitution polynomials.
More precisely, with a polynomial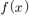 of degree over
of degree over 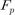 , the proposed algorithm shows the complexity
, the proposed algorithm shows the complexity 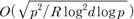 group operations to recover with
group operations to recover with  ,
, 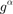 ,
, 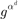 , where
, where 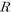 denotes the number of pairs
denotes the number of pairs 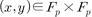 such that
such that 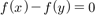 . As an example using the Dickson polynomial, we reveal
. As an example using the Dickson polynomial, we reveal 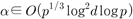 group operations when
group operations when 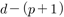 .
.
In this talk, we propose a new approach to solve DLPwAI concentrating on the behavior of function mapping between the finite fields rather than using an embedding to auxiliary groups. This result shows the relation between the complexity of the algorithm and the number of absolutely irreducible factors of the substitution polynomials, hence enlightens the research on the substitution polynomials.
More precisely, with a polynomial


















